ניתן לפתח באופן גס את הקשר בין המסה לרדיוס של ננס לבן, על ידי שימוש בשיקול של מינימום אנרגיה. ניתן להעריך את האנרגיה של ננס הלבן כסכום של האנרגיה הפוטנציאלית והאנרגיה הקינטית שלו. האנרגיה הפוטנציאלית הכבידתית ליחידת מסה בננס הלבן, Eg, תהיה מסדר הגודל של  , כאשר G הוא קבוע הכבידה M היא מסת הננס הלבן ו-R הוא רדיוסו.
, כאשר G הוא קבוע הכבידה M היא מסת הננס הלבן ו-R הוא רדיוסו.
 , כאשר G הוא קבוע הכבידה M היא מסת הננס הלבן ו-R הוא רדיוסו.
, כאשר G הוא קבוע הכבידה M היא מסת הננס הלבן ו-R הוא רדיוסו.
האנרגיה הקינטית ליחידת מסה בננס הלבן, Ek, מקורה בתנועת האלקטרונים כך שהיא תהיה מסדר הגודל של 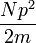 , כאשר p הוא התנע הממוצע האלקטרונים, m היא מסת האלקטרון, ו-N הוא מספר האלקטרונים ליחידת מסה. משום שהחומר בננס הלבן מנוון - כלומר הלחץ שבו נובע מקרבת הפרמיונים ומעקרון האיסור של פאולי, ניתן להעריך כי p הוא מסדר הגודל של האי-ודאות בתנע, Δp; כעת, לפי עקרון אי הוודאות מכפלת אי-הוודאות במיקומו של חלקיק באי-הוודאות בתנע שלו גדולה מקבוע פלאנק המצומצם (ħ). אי-הוודאות במקום, Δx תהיה מסדר הגודל של המרחק הממוצע בין האלקטרונים - n-1/3 (כאשר n הוא מספר האלקטרונים ליחידת נפח). משום שיש N×M אלקטרונים בננס הלבן, והנפח פרופורציוני ל- R³, מספר האלקטרונים ליחידת נפח יהיה פרופורציוני ל-
, כאשר p הוא התנע הממוצע האלקטרונים, m היא מסת האלקטרון, ו-N הוא מספר האלקטרונים ליחידת מסה. משום שהחומר בננס הלבן מנוון - כלומר הלחץ שבו נובע מקרבת הפרמיונים ומעקרון האיסור של פאולי, ניתן להעריך כי p הוא מסדר הגודל של האי-ודאות בתנע, Δp; כעת, לפי עקרון אי הוודאות מכפלת אי-הוודאות במיקומו של חלקיק באי-הוודאות בתנע שלו גדולה מקבוע פלאנק המצומצם (ħ). אי-הוודאות במקום, Δx תהיה מסדר הגודל של המרחק הממוצע בין האלקטרונים - n-1/3 (כאשר n הוא מספר האלקטרונים ליחידת נפח). משום שיש N×M אלקטרונים בננס הלבן, והנפח פרופורציוני ל- R³, מספר האלקטרונים ליחידת נפח יהיה פרופורציוני ל- 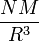 .
.
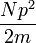 , כאשר p הוא התנע הממוצע האלקטרונים, m היא מסת האלקטרון, ו-N הוא מספר האלקטרונים ליחידת מסה. משום שהחומר בננס הלבן מנוון - כלומר הלחץ שבו נובע מקרבת הפרמיונים ומעקרון האיסור של פאולי, ניתן להעריך כי p הוא מסדר הגודל של האי-ודאות בתנע, Δp; כעת, לפי עקרון אי הוודאות מכפלת אי-הוודאות במיקומו של חלקיק באי-הוודאות בתנע שלו גדולה מקבוע פלאנק המצומצם (ħ). אי-הוודאות במקום, Δx תהיה מסדר הגודל של המרחק הממוצע בין האלקטרונים - n-1/3 (כאשר n הוא מספר האלקטרונים ליחידת נפח). משום שיש N×M אלקטרונים בננס הלבן, והנפח פרופורציוני ל- R³, מספר האלקטרונים ליחידת נפח יהיה פרופורציוני ל-
, כאשר p הוא התנע הממוצע האלקטרונים, m היא מסת האלקטרון, ו-N הוא מספר האלקטרונים ליחידת מסה. משום שהחומר בננס הלבן מנוון - כלומר הלחץ שבו נובע מקרבת הפרמיונים ומעקרון האיסור של פאולי, ניתן להעריך כי p הוא מסדר הגודל של האי-ודאות בתנע, Δp; כעת, לפי עקרון אי הוודאות מכפלת אי-הוודאות במיקומו של חלקיק באי-הוודאות בתנע שלו גדולה מקבוע פלאנק המצומצם (ħ). אי-הוודאות במקום, Δx תהיה מסדר הגודל של המרחק הממוצע בין האלקטרונים - n-1/3 (כאשר n הוא מספר האלקטרונים ליחידת נפח). משום שיש N×M אלקטרונים בננס הלבן, והנפח פרופורציוני ל- R³, מספר האלקטרונים ליחידת נפח יהיה פרופורציוני ל- 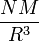 .
.
אם כן, האנרגיה הקינטית ליחידת מסה, Ek היא:
הננס הלבן יהיה בשיווי משקל כאשר האנרגיה הכוללת שלו, Ep+Ek תהיה מינימלית. בשלב זה, האנרגיה הקינטית והאנרגיה הפוטנציאלית תהיינה מאותו סדר גודל. לכן:
כאשר מבודדים את R, רדיוס הננס הלבן, מקבלים:
לכן, הקשר בין רדיוס הננס הלבן למסתו הוא:
דהיינו, הרדיוס פרופורציוני ביחס הפוך לחזקה השלישית של מסת הננס הלבן.
הפתרון משתמש בנוסחה הלא יחסותית  , ולכן היחס המתקבל אינו יחסותי. על מנת לנתח את המערכת עבור אלקטרונים הנעים במהירות הקרובה למהירות האור האנרגיה הקינטית של האלקטרונים תהיה בקירוב
, ולכן היחס המתקבל אינו יחסותי. על מנת לנתח את המערכת עבור אלקטרונים הנעים במהירות הקרובה למהירות האור האנרגיה הקינטית של האלקטרונים תהיה בקירוב  (מכפלת התנע במהירות האור) לכן:
(מכפלת התנע במהירות האור) לכן:
 , ולכן היחס המתקבל אינו יחסותי. על מנת לנתח את המערכת עבור אלקטרונים הנעים במהירות הקרובה למהירות האור האנרגיה הקינטית של האלקטרונים תהיה בקירוב
, ולכן היחס המתקבל אינו יחסותי. על מנת לנתח את המערכת עבור אלקטרונים הנעים במהירות הקרובה למהירות האור האנרגיה הקינטית של האלקטרונים תהיה בקירוב  (מכפלת התנע במהירות האור) לכן:
(מכפלת התנע במהירות האור) לכן:
אם משווים את גודל זה לאנרגיה הפוטנציאלית, מתקבל ש-R מצטמצם ויוצא שהמסה חייבת להיות:
על מנת לפרש תוצאה זו, יש לשים לב לכך שכאשר מסת הננס הלבן גדלה, רדיוסו קטן. לכן, לפי עקרון אי הוודאות, התנע גדל, כלומר המהירות של האלקטרונים גדלה. כאשר המהירות הזו מתקרבת למהירות האור, הביטוי הנ"ל מדויק יותר, כלומר המסה של הננס הלבן מגיעה למסתו הגבולית. על כן, מסתו המרבית של ננס לבן היא Mlimit - מסה גבוהה מזו פירושה שהאלקטרונים ינועו במהירות העולה למהירות האור, בניגוד לעקרונות תורת היחסות.
ניתן להגיע לקשר מדויק יותר באמצעות פיתוח של משוואת מצב עבור הננס הלבן. ממשוואה זו עולה הקשר בין הצפיפות ללחץ בחומר של הננס הלבן. אם הלחץ והצפיפות קבועים כפונקציה של המרחק מהמרכז, אזי פתרון מערכת המשוואות של המשוואה ההידרוסטטית ושל משוואת המצב ייתן את מבנה הננס הלבן בשיווי משקל. לפי הפיתוח הלא יחסותי מקבלים שהרדיוס פרופורציוני ביחס הפוך לשורש השלישי של המסה. תיקונים יחסותיים מגלים שהרדיוס של הננס הלבן מתאפס בגבול מסה סופי. הגבול הזה הוא גבול צ'נדראסקאר - הגבול שבו הננס הלבן כבר לא נתמך על ידי לחץ הניוון של האלקטרונים.
כל החישובים הללו מתייחסים לננס לבן שאינו סב על צירו. אם הננס הלבן מסתובב, המשוואה ההידרוסטטית חייבת לקחת בחשבון את הכוח הצנטריפוגלי המדומה הנובע ממערכת הייחוס הלא אינרציאלית המסתובבת. עבור ננס לבן המסתובב במהירות אחידה וקצובה, גבול המסה המרבית גדל אך במעט. אם הננס הלבן מסתובב בקצב שאינו אחיד ומזניחים את השפעת הצמיגות, אזי, כפי שקבע פרד הויל ב-1947, לא קיים חסם עליון למסתו, כך שמתקיים שיווי משקל סטטי.



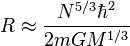


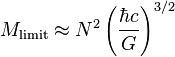
אין תגובות:
הוסף רשומת תגובה